以下は5Gで用いられることになるだろう、いくつかの基地局アンテナ(3.7/4.5GHz帯5Gスモールセル基地局(送信)、4.5GHz帯5Gマクロセル基地局(送信)、28GHz帯5G基地局(送信))について、それらから放射される電波の電力密度を計算する場合の手引きです。
一番初歩の概念から説明していますので、根気よく読めば、どなたにでもおわかりいただけると思います。
先に結果を知りたい方は こちら をご覧下さい。
電波の強さを知ることについて
「電波の強さ」はどう定義され、どう計算されるのでしょうか?
ここではもっとも基本となる概念をごく簡単に紹介して解説し、「電波の強さ」という本来でしたら様々な因子が複雑に関係して決まるだろう事柄を、もっとも単純な条件のもとではどうなるか―つまりどう計算できるか―についてだけ、示してみたいと思います。
実際の環境においては、ある特定の地点での電波の強さは、周辺の様々な電波発信源の諸元(周波数や出力や指向性にかかわる「利得」など)がすべてわかったとしても、計算だけで正確に求めることは難しく―建物や樹木などの遮蔽、それぞれの電波の反射や回折、複数の電波の重ね合わせ、などが起こるためです―、実測してはじめて把握できるわけですが、その大まかな強さ、つまり今現在私たちが環境中で曝露している典型的なケースに比べて桁がどれくらい違った大きさになるのかは、単純化したケースでの計算の結果からでも、推定できると考えられるからです。
電波の「電力密度」という捉え方
電波は、自由空間(物質のない理想の空間)ではエネルギーが衰えることはない、という考え方を出発点にします。ある1点から放射された電波は、本来、無限遠に、どこまでも伝わっていくのです。ただ、電波は放射点から拡散しながら伝わるので、放射点からの距離が異なれば単位面積当たりの「電波のエネルギー」(これを「電力」で表します)の密度が異なることになります。言い換えるなら、電波の電力密度は、電波の「強」「弱」に相当するものです。
実際用いる電波は、送信側のアンテナから発せられるのが通例ですから、その発生られる部分を球の中心にみたてて、その中心からあらゆる方向に同等に広がっていく―これを「等方性」と言います―電波を、中心からある距離だけ離れた場所において、その場所(である一点)を含み込む球面を通過していくものとして捉えることができます。つまり、電力Pをもつ電波は、等方性を示すアンテナがあれば、そこからら四方八方へ飛ぶわけですが、電力Pは距離dを半径とする球の表面積Sに広がる、と考えるわけです。そこで、単位面積当たりの電力(=電力密度)をPDとすると、球の表面積S=4πd2ですから、電力密度PDは、電力Pを、通信距離dを半径とした球の表面積4πd2で割った値になります。これを簡単に言うと、「電波は距離の2乗に比例して減衰する」ということになります。例えば、距離が2倍になると面積は4倍になるので、電波の電力密度は1/4になるわけです。
【公式1】放射源からdだけ離れた位置にある場所での電力密度
PD[電力密度]=Pt[放射源から発せられる電波の電力]÷4πd2 ……①
電波の伝わり方を考える際にややこしいことの一つは、人工衛星局でもない限り、地上で開局されている無線局(放送局、基地局、人が携帯しているので位置が固定されない移動局など)は、大地という反射面が常に存在していて、自由空間とはみなせない、という点です。つまり、放射源から直進して直接届く電波(直接波と言います)のみならず、大地に反射して届く電波も足し合わせて考えねばならない場合がほとんどなのです。ただここでは、この大地反射という要素を取り込むと計算がそれだけ複雑になりますから、自由空間が成立していると仮定して話をすすめます。電波の大まかな強さを知るにはそれでも問題ないからです。
アンテナの指向性と利得
先ほど、電磁波(電波でも光でも)を出す「等方性のアンテナ」について言及しましたが、この「等方的」というのは英語のisotropic(アイソトロピック)の訳語であり、簡単に言うと「どの方向にも同じ強さで放射する(あるいはそれを受け取る感度を有する)」、別の言葉では「完全無指向性」(どれか特別な方向にだけ強くなるということはない)ということです。現実のアンテナは、じつは放射される電波の強さが最大になる放射方向が存在し、それをアンテナの「指向性」と呼びます。そして電力でみたときのその方向の重み付けのために「利得」という概念(ここでは絶対利得G:その方向では等方的放射源の何倍の強さになるか、という指標)を用います。
利得は定義上、指向性を持ったアンテナから飛んでくる電波が、まさに指向性に応じて電波の電力が一番強くなる方向で放射されることになる電力の大きさを決めるものですから、次の公式が成り立つことになります。
【公式2】送信アンテナに送信電力Pを供給した時、送信アンテナの絶対利得をGとすると、送信アンテナから空間に放射される電力の大きさは P☓G となる。
Pt[放射源から発せられる電波の電力]=P[送信アンテナ供給電力]☓G[絶対利得]
……②
「送信アンテナに供給される電力=送信機の出力」か?
ちょっとややこしいことに、電波を発する機械である送信機は、ある電源に繋がれていて、そこからアンテナに与える電力量をボリュームによって調整できるわけですが、機械の中ではアンテナに電力を供給するための仕組みが備えられていて、電源から得ている電力がそこですでにいくらか消費されることになります。これを「給電線系の損失」(Lw)と呼びます。したがって、
「送信機の出力」(P)
→「給電線損失」(Lw)分が失われる
→その残りが「送信アンテナ供給電力」(Pt)となり、アンテナに与えられる
→指向性(「利得G」)に応じて実際にアンテナから放射される電波の電力が決まる
という流れになります。
アンテナのことを日本語ではさらに「空中線」ということがありますから、それを使って言葉を整えると、次のように表現されます。ここで言う「空中線入力電力」とは「送信アンテナに(電波を送り出すために入ってくる)電力」のことですから、これまで使ってきた「送信アンテナ供給電力」と同じ意味となります。
【公式3】
[空中線入力電力(送信アンテナ供給電力)]=[送信機出力]-[給電線損失]
P=Pt-Lw ……③
また、【公式2】で述べたPt(放射源から発せられる電波の電力)は、「空中線に供給される電力に、与えられた方向における空中線の相対利得を乗じたもの」(電波法施行規則第2条第1項第78号)に相当する、電波法でよく用いられている「実効輻射電力(ERP:Effective Radiation Power)」という概念と同じ意味になります。(「輻射」は「放射」と同義です。「実効」という言葉を用いているのは、実際にそのアンテナから出される電波の電力の大きさを表すから、という意味です。)すなわち、
【公式4(内容は公式2と同じ)】
ERP[実効輻射電力]=P[空中線入力電力]☓G[絶対利得]
……④
電力を扱う際のデシベルとは
電波や電力を論じる際には欠かせないのだけれど、一般の人には非常にわかりにくく煩わしいのが、「デシベル」という表記法です(「単位」とも言えそうですが、メートルやグラムなどの物理量ではなく、比率や倍率を表す相対的なもので、その意味では%などと同じです)。
ただありがたいことに、「対数」という高校で習う数学を覚えてさえいれば、その定義はいたってシンプルですから、わかりにくくなるたびにこの定義に戻ることで解決はします。
【公式5】
ある電力P2の大きさをデシベルで表示するとは、基準となるP1と比べることで次の対数で表すことである。
dB=10log10(P2/P1) P1:基準となる電力 P2:(基準と比較する)対象となる電力
……⑤
対数ですから、dBから電力(倍)への換算は次のようになります。
P2/P1=10(dB/10)
多くの場合、【公式5】で言う基準となる電力を1mWにとって(1ミリワット)
1mW=0dBm
と定めますから、換算がずいぶん楽になります。
ただここで「あれっ? dBとdBmと2つ出てきた。これはどう違うのか?」と当然疑問に思われるでしょう。じつは、この「m」がdBの後ろにくっついた表記こそ、「今使っているのは、1ミリワット(mW)を基準したデシベル表示なのですよ」ということを示しているのです。
補足
この「後ろにくっつける」というやり方は結構いろいろな場合に使われていて、例えば、この先の混乱を避けるために先に例を挙げておくと、dBiとdBdというのがあります。これは、これはじつは、「何を基準にして利得を決めているか」の違いが反映しているのです。つまり、
・アイソトロピック・アンテナ(実在しない理想のアンテナ:頭文字はi)を基準にした利得を「絶対利得」という
・半波長(波長をλで表すことが多いので、λ/2の長さを持つ)ダイポール・アンテナ(よく目にする、T字型アンテナのTの字の上の棒「―」が半波長の長さになっているアンテナ:
頭文字はd )を基準にした利得を「相対利得」という区別をしているだけであり、それぞれの表記は、絶対利得がdBi(「でーびーあい」と読む)、相対利得が単にdBd(「でーびーでー」と読む)になります。当然、半波長ダイポール・アンテナもdBiで表記できます。その値は実測で決めることができ、絶対利得2.14 dBiとなります。添え字(iやd)を省いて単に利得○○ dBと書くときがありますが,一般的には絶対利得を指します。
デシベルのイメージをつかむために、いくつかの代表的な換算を覚えておく、というやり方がいいように思います。
無線電波の世界ではdBm(ディービーエム)がよく用いられ、これは1mWを基準とするものですから、定義上1mW=0dBm となります。
【公式5】を見ればわかるように、「10を底とする対数(=常用対数)」が使われていることから、次のような概算がただちにできることになるのです。
私たちは日頃用いている10 進数は10 倍ごとに桁を進める方式です。これは底が10 の指数関数にあたるので、対数関数も底を10 とするlog10 x を考えると便利なことが多いので、底が10 の対数を「常用対数」と呼んでいるわけです。
対数の性質からlog10 1 = 0、log10 10 = 1 なので、log10 2 やlog10 5 は0 と1 の間の値であることは間違いないのはわかります。ではそれは計算できるのでしょうか?
たとえば210 = 1024 であるから、210 ≈ 1000 = 103 と考えてみましょう(「≈」というのは「ほぼ等しい」という意味の記号)。すると両辺の常用対数をとることで
log10 210 ≈ log10 103
がいえますが、対数の性質からこの関係は
10 log10 2 ≈ 3
に書き換えられることになります。そこで、両辺を10 で割ってlog10 2 ≈ 3/10= 0.3であることがわかります。一方で、
log10 2 + log10 5 = log10(2 × 5) = log10 10 = 1
だから、log10 2 ≈ 0.3 であればlog10 5 ≈ 0.7 であることもわかります。
10 log10 2 ≈ 3 が何を意味するかというと、
「電力の2倍 ←→ 3dBのアップ(+3dB)」
「電力の1/2 ←→ 3dBのダウン(-3dB)」
になる、ということです。
同様に 10dB は「10倍」、-10dBは1/10倍となります。
すると、10dBと3dBの倍率を覚えておけば、
13dB=10dB+3dB=10倍×2倍=20倍
14dB=10dB+10dB-3dB-3dB=10倍×10倍÷2倍÷2倍=25倍
など、ほとんどの数値変換が可能となるのです。
デシベル表示の電波諸元を使っての電力密度の計算
さて、桁数が何桁にもなる数値を扱うことが多い電波の世界では、数値の計算もこのデシベル表示を用いたまま行うことが慣例となっています。
そこで、デシベル表示を使った実際の電波の諸元データを用いて、電波の強さを計算してみましょう。
5Gに関わって電波諸元が数値として示されているのは、次の資料だけだと思われますので、それを用います。
「3.7GHz帯, 4.5GHz帯, 28GHz帯における5G導入に係る周波数共用検討」
のなかの
3.7/4.5GHz帯5Gスモールセル基地局(送信)(5ページ)
4.5GHz帯5Gマクロセル基地局(送信)(8ページ)
28GHz帯5G基地局(送信)(24ページ)
です。これらが、5Gで用いられる地上の固定局の基地局の種類とそれぞれの種類に応じた発信電波の諸元になります。
では、上記資料の5ページの表を読み解いてみましょう。
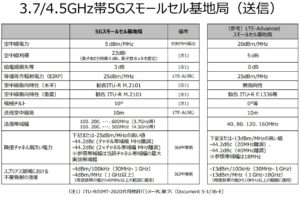
まず、この表の左(「5Gスモールセル基地局」)と右((参考)LTE-Advancedスモールセル基地局)のどちらでも
「空中線電力」(dBm/MHz)+「空中線利得」(dBi)-「給電線損失等」(dB)
=「等価等方輻射電力」(dBm/MHz)
になっていることに注目してください。
これは【公式3】と【公式4】に対応しています(この表ではすべてデシベル表示になっていることに注意)。
デシベル表示では、何倍分大きくなる(+)小さくなる(-)を対数で表していますから、それを「足し算・引き算」して最終的に何倍分になるかを求めることができます。
等価等方輻射電力EIRP(Equivalent Isotropic Radiation Power)というのは、実効輻射電力がアイソトロピック・アンテナを基準とした時の電力を指す場合に使う用語です。先に紹介した実効輻射電力ERPは、ダイポール・アンテナを基準にした電力ですので、「Isotropic」という単語を抜いているだけです。この使い分けがあるため
EIRP(等価等方輻射電力):空中線電力にアンテナ絶対利得(G)を乗じたもの
ERP(実効輻射電力):空中線電力にアンテナ相対利得(G’)を乗じたもの
となり、デシベルの式でそれを表すと、
EIRP[dBm]=Pt[dBm]+G[dBi]= P[dBm]+G[dBi]-Lw[dB]
ERP[dBm]=Pt[dBm]+G[dBd]= P[dBm]+G’[dBd]-Lw[dB]
となります。
次に、空中線電力の表し方として、[dBm/MHz]が用いられていますが、デシベル表示はわかるとしても、[/MHz]の意味がわかりにくいかと思われます。EIRPにしろERPにしろ、実際の電波の強さは刻々に変化するものですから、周波数のある帯域幅ごとに生じる平均的電力量でとらえた大きさを、実施に使用されている周波数の範囲全体をわたって積分することで表示するのが、測定器の原理となっています。空中線電力を表す場合は単位周波数として1 MHzを使うのが原則です。例えば “10mW/MHz” のように表記することになりますが、もしこの空中線電力で1.5GH帯の携帯電話が使われたとするなら、実際の空中線電力はいくらになるのでしょうか。問題はその1.5GHzという周波数ではなくて、あくまで中心帯域を示すにすぎないその1.5GHzの前後でどれくらいの幅で電波を使用しているか、ということになります。例えば1.5GHz帯とは、およそ1427.9MHz~1510.9MHzの範囲の周波数帯のことであり、第3世代(3G)携帯電話やLTEのサービスが提供されていた時には(今はすべてLTEに割り当てられている)、NTTドコモに15MHz幅、KDDIと当時のソフトバンクモバイル(現ソフトバンク)に10MHz幅が割り当てられていました。そうするとその際の空中線出力の計算は、平均的にみてNTTドコモの場合は10mW/MHz☓15MHz =150mW、ソフトバンクの場合は 10mW/MHz☓10MHz =100mWとみなすことができます。
この考え方が適用できるとすると、5dBm/MHzという上記表の空中線電力の値は、表のなかの「送信帯域幅」として記されている
100、200、・・・、600MHz(3.7GHz帯)
100、200、・・・、500MHz(4.5GHz帯)
という値から、3.7GHz帯にしろ、4.5GHz帯にしろ、100MHzという帯域幅を使っていることがみてもれますから(例えば、「3.7GHz帯」の場合、3.4-3.5GHz, 3.5-3.6GHz, 3.6-3.7GHz, 3.7-3.8GHz, 3.9-4.0GHz, 4.0-4.1GHzという100MHz幅区切りの6つの帯域)、5dBmという値に100をかけた数が実際の空中線電力になるはずです。ただし、この5dBmは、表のなかで「EIRPから算出」と記されていて、そのEIRPは「LTE-Advancedスモールセル基地局と同じ」となっていますから、「EIRPは今使っているにLTE-Advancedスモールセル基地局と同じにした」という条件のもとで、新しいアンテナを新しい周波数帯で用いた場合には、次のようになることがわかります。(アンテナの指向性が高いために利得が随分大きくなっていることに注目してください。ビームフォーミンが使われるからだと思われます。)
空中線電力 5dBm/MHz×100MHz=3.16mW/MHz×100MHz=316mW
等価等方輻射電力(EIRP)25dBm/MHz ×100MHz=316mW×100mW/MHz=31600mW
後者は、前者の値から「供給電力線損失」と「利得」を加味して計算して出すのですから(空中線利得23dBiは「約199倍」、供給電力線損失3dBは「約1.99分の1」)、結局、316mW×199÷1.99=3160mWで同じになります。
するといよいよ、この値を用いて【公式1】から、この送信アンテナからある距離だけ離れた地点での電力密度が求められることになります。
ここでは例えば、基地局高さ10m、受信機の高さを身長2メートルの人の高さと仮定して2mとすると、アンテナと人との垂直距離は8mになります。さらに水平距離が20m離れていると仮定すると、三平方の定理からアンテナから人までの21.54mほどになります。
よって、【公式1】より
31600mW÷[4π(21.54m)×(21.54m)]=31600000μW÷(4×3.14×2154cm×2154cm)
=0.54μW/cm2
となることがわかります。
以下、同じ計算方法で3.7/4.5GHz帯5Gスモールセル基地局(送信)(5ページ)、4.5GHz帯5Gマクロセル基地局(送信)(8ページ)、28GHz帯5G基地局(送信)(24ページ)について計算した結果を以下に示しておきます。
これらの値(上記の表では0.2から2.4 μW/cm2という計算結果になっています)は、現在用いられている携帯基地局の電波の強さと比べた場合、どれくらい大きいと言えるのでしょうか? 総務省が公表しているパンフレット「電波と安心な暮らし 携帯基地局編 携帯電話基地局とわたしたちの暮らし」の6ページには現行の基地局電波の電力密度の一例が掲げられていますが、「200mの位置が指向方向となる場合での一般的な計算例」として最も強くなる場所での電力密度として0.8μW/cm2が掲げられています。5Gでの上記4種類の基地局アンテナから放射される電波が、かなり多くの周辺の地点で、この0.8μW/cm2に匹敵するような値になり、場所によってはそれより数倍程度は大きくなることも想定できる、と言えそうです。